Caída libre ideal
Véase también: Ecuaciones para un cuerpo en caída libre
En la caída libre ideal, se desprecia la resistencia aerodinámica que presenta el aire al movimiento del cuerpo, analizando lo que pasaría en elvacío. En esas condiciones, la aceleración que adquiriría el cuerpo sería debida exclusivamente a la gravedad, siendo independiente de su masa; por ejemplo, si dejáramos caer una bala de cañón y una pluma en el vacío, ambos adquirirían la misma aceleración,  , que es la aceleración de la gravedad.
, que es la aceleración de la gravedad.
 , que es la aceleración de la gravedad.
, que es la aceleración de la gravedad.Ecuación del movimiento
De acuerdo a la segunda ley de Newton, la fuerza  que actúa sobre un cuerpo es igual al producto de su masa
que actúa sobre un cuerpo es igual al producto de su masa  por la aceleración que adquiere. En caída libre sólo intervienen el peso
por la aceleración que adquiere. En caída libre sólo intervienen el peso  (vertical, hacia abajo) y el rozamiento aerodinámico
(vertical, hacia abajo) y el rozamiento aerodinámico 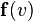 en la misma dirección, y sentido opuesto a la velocidad. Dentro de un campo gravitatorio aproximadamente constante, la ecuación del movimiento de caída libre es:
en la misma dirección, y sentido opuesto a la velocidad. Dentro de un campo gravitatorio aproximadamente constante, la ecuación del movimiento de caída libre es:
 que actúa sobre un cuerpo es igual al producto de su masa
que actúa sobre un cuerpo es igual al producto de su masa  por la aceleración que adquiere. En caída libre sólo intervienen el peso
por la aceleración que adquiere. En caída libre sólo intervienen el peso  (vertical, hacia abajo) y el rozamiento aerodinámico
(vertical, hacia abajo) y el rozamiento aerodinámico 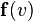 en la misma dirección, y sentido opuesto a la velocidad. Dentro de un campo gravitatorio aproximadamente constante, la ecuación del movimiento de caída libre es:
en la misma dirección, y sentido opuesto a la velocidad. Dentro de un campo gravitatorio aproximadamente constante, la ecuación del movimiento de caída libre es:
La aceleración de la gravedad  lleva signo negativo porque se toma el eje vertical como positivo hacia arriba.
lleva signo negativo porque se toma el eje vertical como positivo hacia arriba.
 lleva signo negativo porque se toma el eje vertical como positivo hacia arriba.
lleva signo negativo porque se toma el eje vertical como positivo hacia arriba.Trayectoria en caída libre
Caída libre totalmente vertical
El movimiento del cuerpo en caída libre es vertical con velocidad creciente (aproximadamente movimiento uniformemente acelerado con aceleracióng) (aproximadamente porque la velocidad aumenta cuando el objeto disminuye en altura, en la mayoría de los casos la variación es despreciable). La ecuación de movimiento se puede escribir en términos la altura y:
(1)
donde:
 , son la aceleración y la velocidad verticales.
, son la aceleración y la velocidad verticales. , es la fuerza de rozamiento fluidodinámico (que aumenta con la velocidad).
, es la fuerza de rozamiento fluidodinámico (que aumenta con la velocidad).
- Si, en primera aproximación, se desprecia la fuerza de rozamiento, cosa que puede hacerse para caídas desde pequeñas alturas de cuerpos relativamente compactos, en las que se alcanzan velocidades moderadas, la solución de la ecuación diferencial () para las velocidades y la altura vienen dada por:
donde v0 es la velocidad inicial, para una caída desde el reposo v0 = 0 y h0 es la altura inicial de caída.











 es constante; esto significa que no existe aceleración.
es constante; esto significa que no existe aceleración. en cualquier instante
en cualquier instante  viene dada por
viene dada por .
.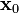 y un tiempo inicial
y un tiempo inicial 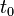 , ambos distintos de cero, la posición para cualquier tiempo está dada por
, ambos distintos de cero, la posición para cualquier tiempo está dada por