martes, 29 de septiembre de 2015

Estado de agregación de la materia

Este diagrama muestra la nomenclatura para las diferentes transiciones de fase sureversibilidad y relación con la variación de la entalpía.

En física y química se observa que, para cualquier sustancia o mezcla, modificando sus condiciones de temperatura o presión, pueden obtenerse distintos estados o fases, denominados estados de agregación de la materia, en relación con las fuerzas de unión de las partículas (moléculas, átomos o iones) que la constituyen.

Todos los estados de agregación poseen propiedades y características diferentes; los más conocidos y observables cotidianamenteson cuatro, llamados fases sólida, líquida, gaseosa y plasmática. También son posibles otros estados que no se producen de forma natural en nuestro entorno, por ejemplo: condensado de Bose-Einstein, condensado fermiónico y estrellas de neutrones. Se cree que también son posibles otros, como el plasma de quark-gluón.¹

Estado sólido

Artículo principal: Sólido

Los objetos en estado sólido se presentan como cuerpos de forma definida; sus átomos a menudo se entrelazan formando estructuras estrechas definidas, lo que les confiere la capacidad de soportar fuerzas sin deformación aparente. Son calificados generalmente como duros y resistentes, y en ellos las fuerzas de atracción son mayores que las de repulsión. En los sólidos cristalinos, la presencia de espacios intermoleculares pequeños da paso a la intervención de las fuerzas de enlace, que ubican a las celdillas en formas geométricas. En los amorfos o vítreos, por el contrario, las partículas que los constituyen carecen de una estructura ordenada.

Las sustancias en estado sólido suelen presentar algunas de las siguientes características:

Cohesión elevada;
Tienen una forma definida y memoria de forma, presentando fuerzas elásticas restitutivas si se deforman fuera de su configuración original;
A efectos prácticos son incompresibles,
Resistencia a la fragmentación;
Fluidez muy baja o nula;
Algunos de ellos se subliman.

Véase también: Materia granular

Estado líquido

Artículo principal: Líquido

Si se incrementa la temperatura de un sólido, este va perdiendo forma hasta desaparecer la estructura cristalina, alcanzando el estado líquido. Característica principal: la capacidad de fluir y adaptarse a la forma del recipiente que lo contiene. En este caso, aún existe cierta unión entre los átomos del cuerpo, aunque mucho menos intensa que en los sólidos. El estado líquido presenta las siguientes características:

Cohesión menor.
Movimiento energía cinética.
Son fluidos, no poseen forma definida, ni memoria de forma por lo que toman la forma de la superficie o el recipiente que lo contiene.
En el frío se contrae (exceptuando el agua).
Posee fluidez a través de pequeños orificios.
Puede presentar difusión.
Son poco compresibles.

Estado gaseoso

Artículo principal: Gas

Se denomina gas al estado de agregación de la materia que no tiene forma ni volumen definido. Su principal composición son moléculas no unidas, expandidas y con poca fuerza de atracción, haciendo que no tengan volumen y forma definida, provocando que este se expanda para ocupar todo el volumen del recipiente que la contiene, con respecto a los gases las fuerzas gravitatorias y de atracción entre partículas resultan insignificantes. Es considerado en algunos diccionarios como sinónimo de vapor, aunque no hay que confundir sus conceptos, ya que el término de vapor se refiere estrictamente para aquel gas que se puede condensar por presurización a temperatura constante. Los gases se expanden libremente hasta llenar el recipiente que los contiene, y su densidad es mucho menor que la de los líquidos y sólidos.

Dependiendo de sus contenidos de energía o de las fuerzas que actúan, la materia puede estar en un estado o en otro diferente: se ha hablado durante la historia, de un gas ideal o de un sólido cristalino perfecto, pero ambos son modelos límites ideales y, por tanto, no tienen existencia real.

En los gases reales no existe un desorden total y absoluto, aunque sí un desorden más o menos grande.

En un gas, las moléculas están en estado de caos y muestran poca respuesta a la gravedad. Se mueven tan rápidamente que se liberan unas de otras. Ocupan entonces un volumen mucho mayor que en los otros estados porque dejan espacios libres intermedios y están enormemente separadas unas de otras. Por eso es tan fácil comprimir un gas, lo que significa, en este caso, disminuir la distancia entre moléculas. El gas carece de forma y de volumen, porque se comprende que donde tenga espacio libre allí irán sus moléculas errantes y el gas se expandirá hasta llenar por completo cualquier recipiente.

El estado gaseoso presenta las siguientes características:

Cohesión casi nula.
No tienen forma definida.
Su volumen es variable.

Estado plasmático

Artículo principal: Plasma

El plasma es un gas ionizado, es decir que los átomos que lo componen se han separado de algunos de sus electrones. De esta forma el plasma es un estado parecido al gas pero compuesto por aniones y cationes (iones con carga negativa y positiva, respectivamente), separados entre sí y libres, por eso es un excelente conductor. Un ejemplo muy claro es el Sol.

En la baja Atmósfera terrestre, cualquier átomo que pierde un electrón (cuando es alcanzado por una partícula cósmica rápida) se dice que está ionizado. Pero a altas temperaturas es muy diferente. Cuanto más caliente está el gas, más rápido se mueven sus moléculas y átomos, (ley de los gases ideales) y a muy altas temperaturas las colisiones entre estos átomos, moviéndose muy rápido, son suficientemente violentas para liberar los electrones. En la atmósfera solar, una gran parte de los átomos están permanentemente «ionizados» por estas colisiones y el gas se comporta como un plasma.

A diferencia de los gases fríos (por ejemplo, el aire a temperatura ambiente), los plasmas conducen la electricidad y son fuertemente influidos por los campos magnéticos. Lalámpara fluorescente, contiene plasma (su componente principal es vapor de mercurio) que calienta y agita la electricidad, mediante la línea de fuerza a la que está conectada la lámpara. La línea, positivo eléctricamente un extremo y negativo, causa que los iones positivos se aceleren hacia el extremo negativo, y que los electrones negativos vayan hacia el extremo positivo. Las partículas aceleradas ganan energía, colisionan con los átomos, expulsan electrones adicionales y mantienen el plasma, aunque se recombinen partículas. Las colisiones también hacen que los átomos emitan luz y esta forma de luz es más eficiente que las lámparas tradicionales. Los letreros de neón y las luces urbanas funcionan por un principio similar y también se usaron en electrónicas.

Perfil de la ionosfera

La parte superior de la ionosfera se extiende en el espacio algunos cientos de kilómetros y se combina con la magnetosfera, cuyo plasma está generalmente más rarificado y también más caliente. Los iones y los electrones del plasma de la magnetosfera provienen de la ionosfera que está por debajo y del viento solar y muchos de los pormenores de su entrada y calentamiento no están claros aún.

Existe el plasma interplanetario, el viento solar. La capa más externa del Sol, la corona, está tan caliente que no sólo están ionizados todos sus átomos, sino que aquellos que comenzaron con muchos electrones, tienen arrancados la mayoría (a veces todos), incluidos los electrones de las capas más profundas que están más fuertemente unidos. En la corona del Sol se ha detectado la radiación electromagnética característica del hierro que ha perdido 13 electrones.

Esta temperatura extrema evita que el plasma de la corona permanezca cautivo por la gravedad solar y, así, fluye en todas direcciones, llenando el Sistema Solar más allá de los planetas más distantes.

Propiedades del plasma: Hay que decir que hay 2 tipos de plasma, fríos y calientes:

En los plasmas fríos, los átomos se encuentran a temperatura ambiente y son los electrones los que se aceleran hasta alcanzar una temperatura de 5000 °C. Pero como los iones, que son muchísimo más masivos, están a temperatura ambiente, no queman al tocarlos.
En los plasmas calientes, la ionización se produce por los choques de los átomos entre sí. Lo que hace es calentar un gas mucho y por los propios choques de los átomos entre sí se ionizan. Estos mismos átomos ionizados también capturan electrones y en ese proceso se genera luz (por eso el Sol brilla, y brilla el fuego, y brillan los plasmas de los laboratorios).

Condensado de Bose-Einstein[editar]

Artículo principal: Condensado de Bose-Einstein

Esta nueva forma de la materia fue obtenida el 5 de julio de 1995, por los físicos Eric A. Cornell, Wolfgang Ketterle y Carl E. Wieman, por lo que fueron galardonados en 2001 con el Premio Nobel de física. Los científicos lograron enfriar los átomos a una temperatura 300 veces más baja de lo que se había logrado anteriormente. Se le ha llamado "BEC, Bose - Einstein Condensado" y es tan frío y denso que aseguran que los átomos pueden quedar inmóviles. Todavía no se sabe cuál será el mejor uso que se le pueda dar a este descubrimiento. Este estado fue predicho por Satyendra Nath Bose y Albert Einstein en 1926.

Condensado de Fermi

Artículo principal: Condensado fermiónico

Creado en la universidad de Colorado por primera vez en 1999, el primer condensado de Fermi formado por átomos fue creado en 2003. El condensado fermiónico, considerado como el sexto estado de la materia, es una fase superfluida formada por partículas fermiónicas a temperaturas bajas. Está cercanamente relacionado con el condensado de Bose-Einstein. A diferencia de los condensados de Bose-Einstein, los fermiones condensados se forman utilizando fermiones en lugar de bosones.

Dicho de otra forma, el condensado de Fermi es un estado de agregación de la materia en la que la materia adquiere superfluidez. Se crea a muy bajas temperaturas, extremadamente cerca del cero absoluto.

Los primeros condensados fermiónicos describían el estado de los electrones en un superconductor. El primer condensado fermiónico atómico fue creado por Deborah S. Jin en 2003. Un condensado quiral es un ejemplo de un condensado fermiónico que aparece en las teorías de los fermiones sin masa con rotura de simetría quiral.

Elasticidad

Una varilla elástica vibrando, es un ejemplo de sistema donde la energía potencial elástica se transforma en energía cinética y viceversa.

En física el término elasticidad designa la propiedad mecánica de ciertos materiales de sufrir deformaciones reversibles cuando se encuentran sujetos a la acción de fuerzas exteriores y de recuperar la forma original si estas fuerzas exteriores se eliminan.

Introducción

La elasticidad es estudiada por la teoría de la elasticidad, que a su vez es parte de la mecánica de sólidos deformables. La teoría de la elasticidad (TE) como la mecánica de sólidos (MS) deformables describe cómo un sólido (o fluido totalmente confinado) se mueve y deforma como respuesta a fuerzas exteriores. La diferencia entre la TE y la MS es que la primera solo trata sólidos en que las deformaciones son termodinámicamente reversibles y en los que el estado tensiones

\boldsymbol{\sigma}

en un punto

\mathbf{x}

en un instante dado dependen solo de las deformaciones

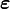\boldsymbol{\varepsilon}

en el mismo punto y no de las deformaciones anteriores (ni el valor de otras magnitudes en un instante anterior). Para un sólido elástico la ecuación constitutiva funcionalmente es de la forma:

$\boldsymbol{\sigma}(\mathbf{x},t) = \hat{T}(\boldsymbol{\varepsilon}(\mathbf{x},t);\mathbf{x}), \qquad \qquad \hat{T}:\mathcal{T}_2(\R^3) \times \R^3 \to \mathcal{T}_2(\R^3)$

donde

\scriptstyle \mathcal{T}_2(\R^3)

denota el conjunto de tensores simétricos de segundo orden del espacio euclídeo. Si el sólido es homogéneo el valor de la función anterior no dependerá del segundo argumento.

La propiedad elástica de los materiales está relacionada, como se ha mencionado, con la capacidad de un sólido de sufrir transformaciones termodinámicas reversibles e independencia de la velocidad de deformación (los sólidos viscoelásticos y los fluidos, por ejemplo, presentan tensiones dependientes de la velocidad de deformación). Cuando sobre un sólido deformable actúan fuerzas exteriores y éste se deforma se produce un trabajo de estas fuerzas que se almacena en el cuerpo en forma de energía potencial elástica y por tanto se producirá un aumento de la energía interna. El sólido se comportará elásticamente si este incremento de energía puede realizarse de forma reversible, en este caso se dice que el sólido es elástico.

Elasticidad lineal

Un caso particular de sólido elástico se presenta cuando las tensiones y las deformaciones están relacionadas linealmente, mediante la siguiente ecuación constitutiva:

$\sigma_{ij} = \sum_{k,l} C_{ijkl}\varepsilon_{kl} \,$

Cuando eso sucede se dice que el sólido es elástico lineal. La teoría de la elasticidad lineal es el estudio de sólidos elásticos lineales sometidos a pequeñas deformaciones de tal manera que además los desplazamientos y deformaciones sean "lineales", es decir, que las componentes del campo de desplazamientos u sean muy aproximadamente una combinación lineal de las componentes del tensor deformación del sólido. En general un sólido elástico lineal sometido a grandes desplazamientos no cumplirá esta condición. Por tanto la teoría de la elasticidad lineal solo es aplicable a:

Sólidos elásticos lineales, en los que tensiones y deformaciones estén relacionadas linealmente (linealidad material).
Deformaciones pequeñas, es el caso en que deformaciones y desplazamientos están relacionados linealmente. En este caso puede usarse el tensor deformación lineal de Green-Lagrange para representar el estado de deformación de un sólido (linealidad geométrica).

Debido a los pequeños desplazamientos y deformaciones a los que son sometidos los cuerpos, se usan las siguientes simplificaciones y aproximaciones para sistemas estables:

Las tensiones se relacionan con las superficies no deformadas
Las condiciones de equilibrio se presentan para el sistema no deformado

Para determinar la estabilidad de un sistema hay presentar las condiciones de equilibrio para el sistema deformado.

Tensión

Componentes del tensor tensión en un punto P de un sólido deformable.

La tensión en un punto se define como el límite de la fuerza aplicada sobre una pequeña región sobre un plano π que contenga al punto dividida del área de la región, es decir, la tensión es la fuerza aplicada por unidad de superficie y depende del punto elegido, del estado tensional de sólido y de la orientación del plano escogido para calcular el límite. Puede probarse que la normal al plano escogido n_π y la tensión t_π en un punto están relacionadas por:

${t_\pi} = {\mathbf{T}(n_\pi)} \,$

Donde T es el llamado tensor tensión, también llamado tensor de tensiones, que fijada una base vectorial ortogonal viene representado por una matriz simétrica 3x3:

$\mathbf{T} = \left( \begin{matrix} \sigma_{xx} & \sigma_{xy} & \sigma_{xz}\\ \sigma_{yx} & \sigma_{yy} & \sigma_{yz}\\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz} \end{matrix} \right) = \left( \begin{matrix} \sigma_x & \tau_{xy} & \tau_{xz}\\ \tau_{yx} & \sigma_y & \tau_{yz}\\ \tau_{zx} & \tau_{zy} & \sigma_z \end{matrix} \right)$

Donde la primera matriz es la forma común de escribir el tensor tensión en física y la segunda forma usa las convenciones comunes en ingeniería. Dada una región en forma deortoedro con caras paralelas a los ejes coordenados situado en el interior un sólido elástico tensionado las componentes σ_xx, σ_yy y σ_zz dan cuenta de cambios de longitud en las tres direcciones, pero que no distorsinan los ángulos del ortoedro, mientras que las componentes σ_xy, σ_yz y σ_zx están relacionadas con la distorsión angular que convertiría el ortoedro en un paralelepípedo.

Deformación[editar]

En teoría lineal de la elasticidad dada la pequeñez de las deformaciones es una condición necesaria para poder asegurar que existe una relación lineal entre los desplazamientos y la deformación. Bajo esas condiciones la deformación puede representarse adecuadamente mediante el tensor deformación infinitesimal o tensor de pequeñas deformaciones (este tensor solo es válido para algunas situaciones, siendo este un caso particular de los tensores de Cauchy-Almansy y Green-Saint-Venant) que viene dada por:

$\mathbf{D} = \begin{pmatrix} \varepsilon_{xx} & \varepsilon_{xy} & \varepsilon_{xz} \\ \varepsilon_{yx} & \varepsilon_{yy} & \varepsilon_{yz} \\ \varepsilon_{zx} & \varepsilon_{zy} & \varepsilon_{zz} \end{pmatrix} = \begin{pmatrix} \varepsilon_{xx} & \frac{1}{2}\gamma_{xy} & \frac{1}{2}\gamma_{xz} \\ \frac{1}{2}\gamma_{yx} & \varepsilon_{yy} & \frac{1}{2}\gamma_{yz} \\ \frac{1}{2}\gamma_{zx} & \frac{1}{2}\gamma_{zy} & \varepsilon_{zz} \end{pmatrix}$

Los componentes de la diagonal principal contienen los alargamientos (dilataciones), mientras que el resto de los componentes del tensor son los medios desplazamientos. Las componentes están linealmente relacionadas con los desplazmientos mediante esta relación:

$\varepsilon_{ij} = {1 \over 2} \left ({\part u_i \over \part x_j} + {\part u_j \over \part x_i}\right )$

Ecuaciones constitutivas de Lamé-Hooke

Las ecuaciones de Lamé-Hooke son las ecuaciones constitutivas de un sólido elástico lineal, homogéneo e isótropo, tienen la forma:

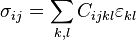
\sigma_{ij} = \sum_{k,l} C_{ijkl}\varepsilon_{kl} \,

En el caso de un problema unidimensional, σ = σ₁₁, ε = ε₁₁, C₁₁ = E y la ecuación anterior se reduce a:

\sigma = E\epsilon \,

Donde E es el módulo de elasticidad longitudinal o módulo de Young y G el módulo de elasticidad transversal. Para caracterizar el comportamiento de un sólido elástico lineal e isótropo se requieren además del módulo de Young otra constante elástica, llamada coeficiente de Poisson (ν) y el coeficiente de temperatura (α). Por otro lado, las ecuaciones de Lamé para un sólido elástico lineal e isótropo pueden ser deducidas del teorema de Rivlin-Ericksen, que pueden escribirse en la forma:

\epsilon_{xx} = \frac{1}{E}\left( \sigma_{xx} - \nu(\sigma_{yy}+\sigma_{zz}) + \alpha\mathcal{4}T \right) \qquad \epsilon_{xy} = \frac{(1+\nu)}{E}\sigma_{xy}= \frac{\sigma_{xy}}{2G}

\epsilon_{yy} = \frac{1}{E}\left( \sigma_{yy} - \nu(\sigma_{xx}+\sigma_{zz}) + \alpha\mathcal{4}T \right) \qquad \epsilon_{yz} = \frac{(1+\nu)}{E}\sigma_{yz} = \frac{\sigma_{yz}}{2G}

\epsilon_{zz} = \frac{1}{E}\left( \sigma_{zz} - \nu(\sigma_{xx}+\sigma_{yy}) + \alpha\mathcal{4}T \right) \qquad \epsilon_{xz} = \frac{(1+\nu)}{E}\sigma_{xz} = \frac{\sigma_{xz}}{2G}

Ciertos materiales muestran un comportamiento solo aproximadamente elástico, mostrando por ejemplo variación de la deformación con el tiempo o fluencia lenta. Estas deformaciones pueden ser permanentes o tras descargar el cuerpo pueden desaparecer (parcial o completamente) con el tiempo (viscoplasticidad, viscoelasticidad). Además algunos materiales pueden presentar plasticidad es decir pueden llegar a exhibir pequeñas deformaciones permanentes, por lo que las ecuaciones anteriores en muchos casos tampoco constituyen una buena aproximación al comportamiento de estos materiales.

Ecuaciones de equilibrio

Equilibrio interno

Cuando las deformaciones no varían con el tiempo, el campo de tensiones dado por el tensor tensión representa un estado de equilibrio con las fuerzas de volumen b = (b_x,b_y,b_z) en todo punto del sólido, lo cual implica que el campo de tensiones satisface estas condiciones de equilibrio:

\frac{\partial \sigma_{xx}}{\partial x}+ \frac{\partial \sigma_{xy}}{\partial y}+ \frac{\partial \sigma_{xz}}{\partial z} + b_x = 0

\frac{\partial \sigma_{yx}}{\partial x}+ \frac{\partial \sigma_{yy}}{\partial y}+ \frac{\partial \sigma_{yz}}{\partial z} + b_y = 0

\frac{\partial \sigma_{zx}}{\partial x}+ \frac{\partial \sigma_{zy}}{\partial y}+ \frac{\partial \sigma_{zz}}{\partial z} + b_z = 0

Equilibrio en el contorno

Además de las últimas ecuaciones deben cumplirse las condiciones de contorno, sobre la superficie del sólido, que relacionan el vector normal a la misma n = (n_x,n_y,n_z) (dirigido hacia el exterior) con las fuerzas por unidad de superficie que actúan en el mismo punto de la superficie f = (f_x,f_y,f_z):

\sigma_{xx}\ n_x+ \sigma_{xy}\ n_y+ \sigma_{xz}\ n_z = f_x

\sigma_{yx}\ n_x+ \sigma_{yy}\ n_y+ \sigma_{yz}\ n_z = f_y

\sigma_{zx}\ n_x+ \sigma_{zy}\ n_y+ \sigma_{zz}\ n_z = f_z

Problema elástico

Artículo principal: Problema elástico

Un problema elástico lineal queda definido por la geometría del sólido, las propiedades de dicho material, unas fuerzas actuantes y unas condiciones de contorno que imponen restricciones al movimiento de cuerpo. A partir de esos elementos es posible encontrar un campo de tensiones internas sobre el sólido (que permitirá identificar los puntos que soportan más tensión) y un campo de desplazamientos (que permitirá encontrar si la rigidez del elemento resistente es la adecuada para su uso).

Para plantear el problema elástico son necesarias las nociones que han sido descritas en las secciones anteriores, que describen las tensiones, las deformaciones y los desplazamientos de un cuerpo. Todas estas magnitudes vienen descritas por 15 funciones matemáticas:

Las seis componentes del tensor de tensiones $\sigma_x, \sigma_y, \sigma_z\;$ y $\sigma_{xy}, \sigma_{yz}, \sigma_{zx}\;$ .
Las tres componentes del vector de desplazamientos: $u_x, u_y,u_z\;$ .
Las seis componentes del tensor de deformaciones: $\varepsilon_x, \varepsilon_y, \varepsilon_z\;$ y $\varepsilon_{xy}, \varepsilon_{yz}, \varepsilon_{zx}\;$ .

Para comprobar si se cumplen estas relaciones, formadas por 15 funciones, el siguiente paso es comprobar si las relaciones descritas hasta ahora bastan para describir completamente el estado de un cuerpo. Una condición necesaria para ello es que el número de ecuaciones disponibles coincida con el número de incógnitas. Las ecuaciones diponibles son:

Las tres ecuaciones de equilibrio de Cauchy.
Las seis ecuaciones de compatibilidad de Saint-Venant, que aseguran que se los desplazamientos y deformaciones están adecaudamente relacionados.
Las seis ecuaciones constitutivas, para un material elástico lineal isótropo y homogéneo estas ecuaciones vienen dadas por las ecuaciones de Lamé-Hooke.

Estas 15 ecuaciones igualan exactamente el número de incógnitas. Un método común es sustituir las relaciones entre desplazamientos y deformaciones en las ecuaciones constitutivas, lo cual hace que se cumplan las ecuaciones de compatibilidad trivialmente. A su vez el resultado de esta sustitución se puede introducir en las ecuaciones de equilibrio de Cauchy lo cual convierte el anterior sistema en un sistema de tres ecuaciones en derivadas paraciales y tres desplazamientos como incógnita.

De esta manera se llega a un sistema de 15 ecuaciones con 15 incognitas. La formulación más simple para resolver el problema elástico es la llamada formulación de Navier, esta formulación reduce el sistema a un sistema de tres ecuaciones diferenciales para los desplazamientos. Esto se logra insertando en las ecuaciones de equilibrio las ecuaciones propias del material, las ecuaciones de los desplazamientos y las ecuaciones de las deformaciones podemos expresar nuestro sistema de ecuaciones en un sistema de tres ecuaciones diferenciales parciales. Si lo reducimos hacia las componentes del vector de desplazamientos llegamos a las ecuaciones de Navier:

G\left[ \frac{\part^2 u_{x}}{\part x^2} + \frac{\part^2 u_{x}}{\part y^2} + \frac{\part^2 u_{x}}{\part z^2} + \frac{1}{1-2 \nu} \frac{\partial}{\partial x} \left( \frac{\partial u_{x}}{\partial x} + \frac{\partial u_{y}}{\partial y} + \frac{\partial u_{z}}{\partial z} \right)\right] + b_{x} = 0

G\left[ \frac{\part^2 u_{y}}{\part x^2} + \frac{\part^2 u_{y}}{\part y^2} + \frac{\part^2 u_{y}}{\part z^2} + \frac{1}{1-2 \nu} \frac{\partial}{\partial y} \left( \frac{\partial u_{x}}{\partial x} + \frac{\partial u_{y}}{\partial y} + \frac{\partial u_{z}}{\partial z} \right) \right] + b_{y} = 0

G\left[ \frac{\part^2 u_{z}}{\part x^2} + \frac{\part^2 u_{z}}{\part y^2} + \frac{\part^2 u_{z}}{\part z^2} + \frac{1}{1-2 \nu} \frac{\partial}{\partial z} \left( \frac{\partial u_{x}}{\partial x} + \frac{\partial u_{y}}{\partial y} + \frac{\partial u_{z}}{\partial z} \right) \right] + b_{z} = 0

Que con el operador Nabla y el operador de Laplace se dejan escribir como:

$G\left[\Delta\mathbf{u} + \frac{1}{1-2\nu} \nabla (\nabla\cdot\mathbf{u})\right] + \mathbf{b} = 0$

Mediante consideraciones energéticas se puede demostrar que estas ecuaciones presentan una única solución.

Elasticidad y diseño mecánico

En ingeniería mecánica es frecuente plantear problemas elásticos para decidir la adecuación de un diseño. En ciertas situaciones de interés práctico no es necesario resolver el problema elástico completo sino que basta con plantear un modelo simplificado y aplicar los métodos de la resistencia de materiales para calcular aproximadamente tensiones y desplazamientos. Cuando la geometría involucrada en el diseño mecánico es compleja la resistencia de materiales suele ser insuficiente y la resolución exacta del problema elástico inabordable desde el punto de vista práctico. En esos casos se usan habitualmente métodos numéricos como el Método de los elementos finitos para resolver el problema elástico de manera aproximada. Un buen diseño normalmente incorpora unos requisitos de:

resistencia adecuada,
rigidez adecuada,
estabilidad global y elástica.